← RU Pythoncursus

L-systemen

Je mag deze opdracht in tweetallen maken! Lever het wel apart in!

In deze opdracht gaan we werken met Lindemeyer-systemen, ofwel L-systemen. Met L-systemen kun je op een simpele manier mooie, recursieve patronen maken. Hieronder staat een voorbeeld, maar er zijn heel veel patronen mogelijk.

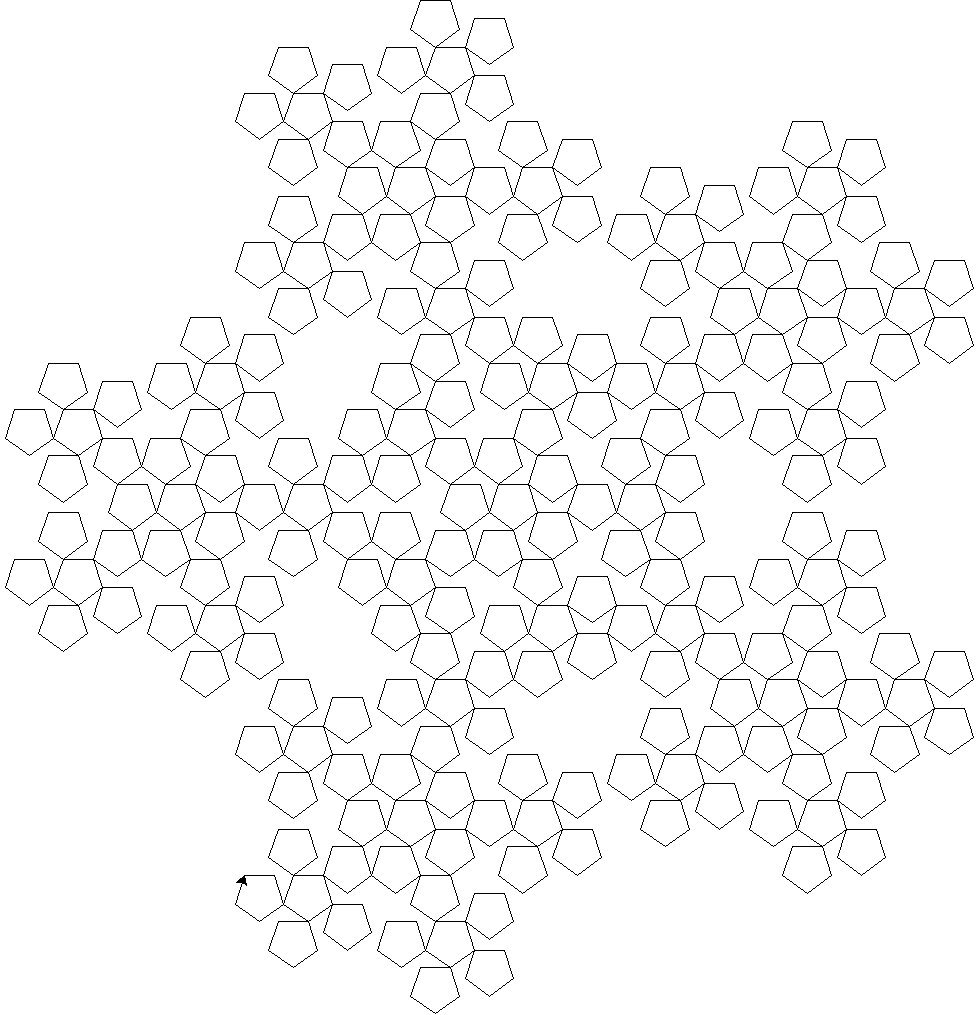
image

Om dit patroon te maken begin je met een simpele string. Deze string wordt een paar keer 'herschreven' volgens een regel, om uiteindelijk een lange string te krijgen die het hele patroon beschrijft. Met Turtlegraphics kun je dit resultaat uiteindelijk tekenen, waarna de bovenstaande figuur ontstaat. In het eerste deel van de opdracht gaan we het bovenstaande voorbeeld tekenen.

Uitleg L-systemen

We gaan nu zelf een L-systeem maken en dit uittekenen met Turtle graphics. Zoals je waarschijnlijk nog wel weet kan de schildpad figuren tekenen door tekenopdrachten als left() of forward() te ontvangen. Met de 'regels' van een L-systeem kunnen we de tekenopdrachten voor de schildpad automatisch genereren. Hierdoor kun je snel hele complexe figuren tekenen.

Het L-systeem bestaat in het algemeen uit een hoek (die de schildpad gaat maken), een lengte (het aantal stapjes dat de schildpad per keer loopt), een diepte (het aantal keer dat we een regel herschrijven) en tenslotte nog de herschrijfregel zelf.

Onderstaande is een voorbeeld van een herschrijfregel: $$ \begin{array}{lcl} F & \rightarrow & F + F - F \end{array} $$

We beginnen met een string $F$. Vervolgens kunnen we de herschrijfregel toepassen en deze $F$ vervangen door de string $F + F - F$. Hierbij zijn $+$ en $-$ geen wiskundige plus en min, maar gewoon tekens in ons herschrijfsysteem. Vervolgens kunnen we weer de herschrijfregel toepassen en weer alle $F$'s vervangen. We krijgen dan:

$$ \begin{array}{lclcl} F + F - F & + & F + F - F & - & F + F - F \end{array} $$

Voor de duidelijkheid staat er extra witruimte tussen de herschreven delen van onze string. Ook deze string kan met de herschrijfregel weer herschreven worden, en zo kunnen we doorgaan. We gaan net zo lang door met het herschrijven van de string totdat de gewenste diepte (die we in ons programma hebben opgegeven) is bereikt.

Opgave

In ons programma gaan we om te beginnen de volgende herschrijfregel gebruiken

$$ \begin{array}{lcl} F & \rightarrow & F - F + + F + F - F - F \end{array} $$

We beginnen met de string $F-F-F-F-F$, en gaan deze herschrijven met bovenstaande regel.

  1. Zet om te beginnen de volgende code in je programma:

    import turtle

hoek = 72
lengte = 10
diepte = 3
start = 'F-F-F-F-F'

  2. Maak de functie herschrijf(S), die een string S ontvangt en deze herschrijft aan de hand van de bovenstaande herschrijfregel. De signatuur van de functie ziet er zo uit:

    def herschrijf(S):
    resultaat = '' # pas hier de herschrijfregel toe
    return resultaat

    Als we de string F-F-F-F-F éénmaal herschrijven, krijgen we:

    F-F++F+F-F-F-F-F++F+F-F-F-F-F++F+F-F-F-F-F++F+F-F-F-F-F++F+F-F-F

    Zorg ervoor dat jouw herschrijf-functie ook dit resultaat geeft.

Nu we een mooie string kunnen genereren, gaan we deze tekenen, namelijk op de volgende manier:

  1. Maak nu de functie teken(S) die de schildpad de string $S$ laat tekenen.

  2. Nu we zowel kunnen herschrijven als tekenen, kun je de figuur bovenaan deze pagina tekenen. Eerst moet je diepte aantal keren herschrijven met de herschrijf-functie. Vervolgens kun je de herschreven string tekenen met de teken-functie.

    Hint: De schildpad zal erg lang bezig zijn met het tekenen van je figuur. Om hem sneller te laten lopen kun je deze code in je programma zetten:

    turtle.speed(0)
turtle.delay(0)

  3. Als het goed is heb je nu een L-systeem getekend. Zo ja, gefeliciteerd! Dit is het einde van het "verplichte" deel van deze opdracht. Mocht je dit leuk vinden, kan je verder gaan met de rest van de opdracht, om nog meer mooie L-systemen te tekenen.

Het bovenstaande voorbeeld heeft maar één herschrijfregel. Er zijn echter ook patronen, die meerdere regels bevatten. In deze regels komen nog meer letters voor dan $F$, $+$ en $-$. Elke regel herschrijft één letter naar een nieuwe string. Bij het herschrijven van een string, moet je dus uitzoeken welk van de regels van toepassing is. Deze extra letters zijn bedoeld om te herschrijven: bij het tekenen hoeft de schildpad met deze letters niets te doen.

  1. Pas je programma aan zodat het volgende L-systeem getekend wordt:

    • hoek = 60
    • diepte = 3 of 4
    • lengte = 10
    • beginstring: $XF$
    • herschrijfregels: $$\begin{array}{lcl} X & \rightarrow & X+YF++YF-FX--FXFX-YF+ \ \end{array}$$ $$\begin{array}{lcl} Y & \rightarrow & -FX+YFYF++YF+FX--FX-Y \end{array}$$

Als je de bovenstaande instructies gevolgd hebt, tekent je programma altijd hetzelfde L-systeem. Het zou mooier zijn als het programma een willekeurig L-systeem kan tekenen. Hieronder staat een lijstje van een aantal bestanden met daarin definities voor L-systemen. De inhoud van deze bestanden heeft de volgorde:

Het aantal herschrijfregels verschilt per L-systeem.

Alleen na deelopdracht 9.:

Je kunt in Firefox, Chrome of een simpele tekstverwerker als Notepad deze bestandjes openen om te zien hoe dit er precies uitziet.

Het openen van een bestand in Python kan zoals in het volgende voorbeeld. Dit voorbeeld leest de regels in als strings, en print ze vervolgens; in jouw programma kun je op dezelfde manier regels inlezen, en ze daarna als L-systeem verwerken.

with open(bestandsnaam) as f:
    eerste_regel = f.readline() # lees regel in als string
    print('regel 1: ' + eerste_regel)
    tweede_regel = f.readline()
    print('en regel 2: ' + tweede_regel)
    # met een for-loop over de rest van de regels:
    for volgende_regel in f:
        print('de rest: ' + volgende_regel)

  1. Schrijf nu een stuk code, dat een bestandje voor een L-systeem opent, en hier de nuttige gegevens uithaalt en opslaat. Je hebt nu dus hoek, regels, etc.

  2. Laat je programma nu een L-systeem uit een bestandje tekenen. Let erop dat de regels goed verwerkt worden: in het bestand staan deze opgeslagen als $F:F+F-F$, maar je programma moet de delen voor en na de dubbele punt natuurlijk scheiden. Je kunt alle bestanden uitproberen: ze maken erg verschillende plaatjes!

We kunnen nu al heel wat soorten L-systemen tekenen. Er zijn ook L-systemen die op planten lijken, en die kunnen we nog niet tekenen. Hiervoor hebben we iets extra's nodig in onze regels, namelijk de tekens $[$ en $]$. In de herschrijfregels werken ze als alle andere tekens. Als we bij het tekenen deze tekens tegenkomen, doen we het volgende:

Hiervoor hebben we een zogenaamde stack nodig, oftewel een stapel: we kunnen iets bovenop de stapel leggen, of we kunnen het bovenste element er weer vanaf pakken om te gebruiken. Zo kunnen we ook posities en richtingen op een stack leggen, om ze te onthouden en later weer op te vragen. Voor de stapel kunnen we gewoon een lijst gebruiken. Iets op de stapel leggen kunnen we dan doen met lijst.append(element), en we kunnen het bovenste element van de stapel pakken met element = lijst.pop().

  1. Zorg dat je tijdens het tekenen een stack bijhoudt van posities en richtingen, en $[$ en $]$ goed verwerkt. Met position() en heading() kun je de huidige positie en richting opvragen, en met setposition(...) en setheading(...) kun je ze op een eerder opgeslagen waarde zetten.

Als je tot dit punt bent gekomen, heb je Python al aardig in de vingers!