← RU Pythoncursus

Inlever optie 1: Sorteren

Zoals je misschien al gezien hebt, kan je in Python lijsten sorteren. Maar het is een goede oefening om dit zelf te kunnen programmeren. We gaan dus een sorteer-algoritme maken, die een lijst van getallen als invoer krijgt en een gesorteerde lijst teruggeeft. In deze opdracht gaan we uit van sorteren van klein naar groot (maar andersom mag ook, dit werkt precies hetzelfde). Er zijn verschillende algoritmes, waarvan de ene efficiënter is dan de andere.

We beginnen met bubble sort, een algoritme dat in kleine, begrijpelijke stapjes werkt. Hierbij ga je van voor naar achteren door de lijst, en je vergelijkt steeds twee (naast elkaar liggende) elementen met elkaar. Als het eerste element groter is dan het volgende, verwissel je ze. Het algoritme zorgt er zo voor dat het grootste getal achteraan komt te staan. Zie de volgende afbeelding, waarbij twee elementen worden verwisseld bij een blauwe pijl, en ze onveranderd blijven bij een rode pijl:

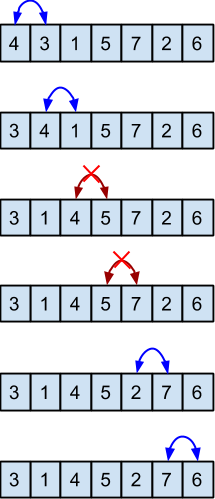
Maak een loop die deze eerste stap van bubble sort uitvoert, waarmee je het grootste element achteraan zet.
Als de stap in de vorige opdracht goed werkt, staat het grootste element op de goede plek. Het ongesorteerde deel van de lijst is nu de hele lijst behalve het laastste element. Voer dezelfde stap op dit ongesorteerde deel uit, om zo ook het op één na grootste getal op de juiste plek te zetten (de tweede plek van achteren).
Het niet-gesorteerde deel van de lijst wordt nu steeds korter, en het gesorteerde deel groeit steeds meer. Voer de code uit vraag 1. uit in een loop, zodat je de hele lijst sorteert. Misschien moet je de code uit opdracht 1. wat aanpassen, om het algoritme goed te laten werken (is bijvoorbeeld de range goed?).
Maak nu een functie die je een lijst als argument kan geven, en die de gesorteerde lijst teruggeeft.
Test je code op willekeurig gevulde lijsten, van een zelfgekozen lengte. Hiervoor kun je de onderstaande code gebruiken. Wat gebeurt er bij een lege lijst?

import random

# genereert een willekeurig gevulde lijst van lengte n
def random_list(n):
    randoms = []
    for _ in range(n):
        randoms.append(random.randrange(10000))
    return randoms

Bubble sort is niet zo'n efficiënt algoritme. Een efficiënter algoritme is merge sort. Hierin speelt recursie een belangrijke rol. Het algoritme werkt als volgt (lees door tot en met 7 voordat je begint met programmeren):

Als je lijst een lengte heeft van $0$ of $1$, dan ben je meteen klaar. Een lijst met minder dan twee elementen kan namelijk nooit in de verkeerde volgorde staan en is dus altijd gesorteerd. Je kunt simpelweg de gegeven lijst weer returnen.
Als de lijst langer is, knippen we hem op in twee helften. We sorteren de twee helften weer met ditzelfde algoritme. Dit is de magie van recursie: als we de rest van ons algoritme goed implementeren, kunnen we er hier op vertrouwen dat dit goed gaat!
We hebben nu twee gesorteerde lijsten, waarvan we één gesorteerde lijst moeten maken. We kunnen een hulpfunctie maken die dit doet.

Opmerking: De recursie werkt, omdat de lijsten die je sorteert steeds kleiner worden. Een lijst van 100 wordt dus opgeknipt in lijsten van 50, die opgeknipt worden in lijsten van 25, etc. Uiteindelijk kom je altijd uit op lijsten van lengte 1. Deze korte lijsten worden apart afgehandeld (zoals hierboven beschreven) en hier stopt de recursie.

We hebben eerst een hulpfunctie nodig om merge-sort aan te kunnen. Deze hulpfunctie krijgt twee gesorteerde lijsten en maakt hiervan één gesorteerde lijst. Maak er gebruik van dat de lijsten al gesorteerd zijn, dat maakt het probleem gemakkelijker!
Maak nu een functie die merge-sort uitvoert. Doe niet meer stappen dan nodig, en vertrouw erop dat je de functie die je aan het maken bent, weer kunt gebruiken voor de kleinere lijsten.
Test het algoritme weer op willekeurig gevulde lijstjes.

Merge-sort is een stuk efficiënter dan bubble-sort. We gaan dit verschil nu visualiseren, door de tijd te meten die nodig is voor het sorteren, en dit in een grafiekje weer te geven. Hiervoor kun je het volgende stukje code gebruiken:

import time

# vraag de huidige tijd op
t = time.time()

Schrijf nu een stukje code dat een aantal (willekeurig gevulde) lijsten gebruikt, hierop beide sorteeralgoritmes uitvoert, en meet hoe lang beide algoritmes duren. Sla deze waarden op in een lijst zodat je met plt een grafiekje kunt tekenen. Teken het grafiekje zodra het meten klaar is, bijvoorbeeld voor de lengtes [100, 200, 400, 800, 1600].
Hoe verlopen de grafieken? Welk algoritme is sneller bij bijvoorbeeld een rij van 2000 elementen?

Als het goed is, zie je dat de tijd om bubble-sort uit te voeren een parabool is. Als de lengte van de lijst $n$ is, is de benodigde tijd dus ongeveer $n^2$. Merge-sort (en enkele andere efficiënte sorteer-algoritmes) kunnen dit in een tijd van ongeveer $n \cdot ^2\text{log}(n)$. Dit neemt natuurlijk minder hard toe dan $n^2$. Hoe groter de lijst, des te belangrijker de snelheid - en des te groter het verschil!